Quantum Noisy Qubits

Subject classification: this is a physics resource.

Formulas for Noisy Qubits

Noisy qubits are a fundamental challenge in current Noisy Intermediate-Scale Quantum (NISQ) computers, where physical qubits are susceptible to errors from decoherence, are sensitive to their environment (noisy), imperfect gate operations, and measurement noise. These errors stem from interactions with the environment and can accumulate during computations, limiting the depth and complexity of algorithms that can be successfully run. Quantum advantage by quantum processors containing up to 1,000 qubits.^[1] Researchers are developing NISQ algorithms that leverage limited resources within these noise constraints and exploring new quantum materials and qubit designs to create more robust qubits for the future of fault-tolerant quantum computing.^[2] How qubits interact with their surrounding environment. Unlike isolated quantum systems, real qubits are affected by noise sources such as stray photons, phonons, or control hardware fluctuations. These interactions cause errors including decoherence^[3] and relaxation that degrade computational performance.

Open system models provide mathematical tools for analyzing and mitigating these effects.^[4]
IBM's 50-qubit quantum computer prototype, as exhibited at CES 2018 in Las Vegas ----->
They describe how methods from the theory of Open quantum system are applied to qubits and quantum hardware. In practice, qubits are never perfectly isolated: they interact with their environments, leading to decoherence, relaxation, and noise that limit computation. This has made open-system tools—such as Kraus operators, Lindblad master equations, and non-Markovian models—fundamental to modern quantum computing research.

Textbooks and surveys treat this intersection as a distinct domain: Breuer & Petruccione’s The Theory of Open Quantum Systems (2002) and Rivas & Huelga’s Open Quantum Systems: An Introduction (2012) present explicit applications to quantum information. Reviews such as Krantz et al., A quantum engineer’s guide to superconducting qubits (2019), and Preskill, Quantum Computing in the NISQ Era and beyond (2018), emphasize that open-system models underpin both noise characterization and the definition of the NISQ regime. Recent tutorials, e.g. Li et al. (2023), treat simulation of open-system dynamics as a computational task in its own right.

As a result, open-system formulations have become central in analyzing qubit performance, setting error-correction thresholds, and guiding fault-tolerant architectures.

Equation used in wave mechanics (see Quantum mechanics) for the wave function of a particle is the time-independent Schrödinger equation

${\displaystyle \nabla ^{2}\psi +{\frac {8\pi ^{2}m}{h^{2}}}(E-U)\psi =0}$

It can also be written in operator form as:

${\displaystyle H\psi =E\psi }$

where ψ is the wave function, ∇² the Laplace operator, h the Planck constant, m the particle's mass, E its total energy, and U its potential energy. It was devised by Erwin Schrödinger, who was mainly responsible for wave mechanics.

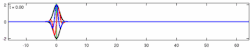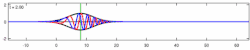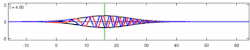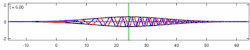
The time-dependent Schrödinger equation (see also Dyson series) for an isolated system is: ${\displaystyle i\hbar {\frac {\partial }{\partial t}}|\psi (t)\rangle =H|\psi (t)\rangle .}$
The unitary propagator is:$${\displaystyle U(t)={\mathcal {T}}\exp \!\left(-{\frac {i}{\hbar }}\int _{0}^{t}H(t')\,dt'\right),}$$with ${\displaystyle {\mathcal {T}}}$ the time-ordering operator.

For open systems, the state of the system alone is obtained from the full density matrix of system+environment:$${\displaystyle \rho _{S}(t)=\mathrm {Tr} _{E}\,[\rho _{SE}(t)].}$$This partial trace generally produces non-unitary dynamics.

Consider a system Hamiltonian (quantum mechanics) ${\displaystyle H_{S}}$, environment Hamiltonian ${\displaystyle H_{E}}$, and an interaction ${\displaystyle H_{I}}$. The total Hamiltonian is:$${\displaystyle H=H_{S}+H_{E}+H_{I}.}$$Even if ${\displaystyle \rho _{SE}}$ evolves unitarily, the reduced density matrix ${\displaystyle \rho _{S}}$ typically obeys an integro-differential equation. Approximations lead to different master equations.

Any completely positive trace-preserving (CPTP) map on a quantum state can be written as:$${\displaystyle {\mathcal {E}}(\rho )=\sum _{k}E_{k}\,\rho \,E_{k}^{\dagger },\qquad \sum _{k}E_{k}^{\dagger }E_{k}=I,}$$where the ${\displaystyle E_{k}}$ are Kraus operators. This is a general representation of open-system dynamics at discrete times.^[5]

Under the Born–Markov approximation (weak coupling and short environment correlation times), the system’s density matrix satisfies the Lindblad master equation:$${\displaystyle {\frac {d\rho }{dt}}=-{\frac {i}{\hbar }}[H,\rho ]+\sum _{k}{\Big (}L_{k}\rho L_{k}^{\dagger }-{\tfrac {1}{2}}\{L_{k}^{\dagger }L_{k},\rho \}{\Big )}.}$$This generator defines a dynamical semigroup (completely positive, trace-preserving evolution).^[6]

For a single qubit, collapse operators commonly model:

• **Relaxation (energy decay):** ${\displaystyle L_{\text{relax}}={\sqrt {\gamma _{1}}}\,\sigma _{-}}$
• **Dephasing:** ${\displaystyle L_{\text{deph}}={\sqrt {\gamma _{\phi }}}\,\sigma _{z}}$

Here ${\displaystyle \gamma _{1}}$ and ${\displaystyle \gamma _{\phi }}$ are the relaxation and dephasing rates, respectively.

If the Markov approximation is not applied, the Redfield equation captures memory effects:$${\displaystyle {\frac {d\rho _{S}(t)}{dt}}=-{\frac {i}{\hbar }}[H_{S},\rho _{S}(t)]-\int _{0}^{t}d\tau \,\mathrm {Tr} _{E}{\big (}[H_{I}(t),[H_{I}(\tau ),\rho _{S}(\tau )\otimes \rho _{E}]]{\big )}.}$$Redfield theory can describe structured environments (e.g. spin baths or photonic reservoirs) but does not guarantee complete positivity without further corrections.^[7]

Spin-exchange collisions between alkali metal atoms can change the hyperfine state of the atoms while preserving total angular momentum of the colliding pair. As a result, spin-exchange collisions cause decoherence There has been significant work on correctly identifying the pointer states in the case of a massive particle decohered by collisions with a fluid environment, A widely used approximation for collisional decoherence assumes exponential suppression of off-diagonal terms:$${\displaystyle C(t)\approx \exp(-\Gamma t),\qquad \Gamma \propto n\,v\,\sigma _{\text{decoh}},}$$with ${\displaystyle n}$ the particle density, ${\displaystyle v}$ the relative velocity, and ${\displaystyle \sigma _{\text{decoh}}}$ the scattering cross-section.^[8]

Open-system formulations are essential in quantum hardware design and analysis:

• **Noise modeling:** Estimating dephasing and relaxation times (${\displaystyle T_{1}}$, ${\displaystyle T_{2}}$) in superconducting qubits and trapped ions.^[9]
• **Error correction:** Providing physical noise models for the design of error-correcting codes.
• **Control techniques:** Informing pulse-shaping and dynamical decoupling sequences to suppress decoherence.
• **Fault tolerance:** Guiding thresholds for quantum error correction using Lindblad-type noise models.

These articles describe the Quantum system as outlined in this article.
Open Quantum System Approaches to Superconducting Qubits
Quantum Computer Operating System: The Key to Quantum Power
Building Quantum Computers A Practical Introduction
OpenQASM: The Quantum Programming Language. Assembly Programming for Quantum Computers
What Are Open Quantum Systems? A Complete Guide
Digital Simulation of Single Qubit Markovian Open Quantum Systems: A Tutorial
Time Evolution in Open Quantum Systems

• The Lindblad approach assumes memoryless noise and may not capture non-Markovian dynamics in advanced devices.
• Redfield and other non-Markovian models can describe richer environments but are computationally expensive and sometimes unphysical.
• Hybrid approaches combining Lindblad and non-Markovian models are under investigation.
• Active error suppression techniques (e.g. dynamical decoupling, error mitigation) complement open-system modeling.

• Quantum
• Quantum A Matter Of Size
• Quantum: A Walk Through the Universe
• Open quantum system
• Quantum decoherence
• Quantum master equation
• Quantum noise
• Density matrix

• Weiss, Ulrich (2012). Quantum Dissipative Systems. World Scientific. ISBN 978-9814374910. 

1. ↑ "Engineers demonstrate a quantum advantage". ScienceDaily. Retrieved 2021-06-29.
2. ↑ "What is Quantum Computing?". TechSpot. 28 June 2021. Retrieved 2021-06-29.
3. ↑ Breuer, Heinz-Peter; Petruccione, Francesco (2002). The Theory of Open Quantum Systems. Oxford University Press. ISBN 978-0199213900. 
4. ↑ Rivas, Ángel; Huelga, Susana F. (2012). Open Quantum Systems: An Introduction. Springer. doi:10.1007/978-3-642-23354-8. ISBN 978-3642233531. 
5. ↑ Nielsen, Michael A.; Chuang, Isaac L. (2010). Quantum Computation and Quantum Information (10th anniversary ed.). Cambridge University Press. ISBN 978-1107002173. 
6. ↑ Lindblad, Göran (1976). "On the generators of quantum dynamical semigroups". Communications in Mathematical Physics 48 (2): 119–130. doi:10.1007/BF01608499. 
7. ↑ Redfield, A.G. (1965). "The Theory of Relaxation Processes". Advances in Magnetic and Optical Resonance 1: 1–32. doi:10.1016/B978-1-4832-3114-3.50007-6. ISBN 978-1-4832-3114-3. ISSN 1057-2732. 
8. ↑ Joos, E.; Zeh, H. D. (1985). "The emergence of classical properties through interaction with the environment". Zeitschrift für Physik B 59 (2): 223–243. doi:10.1007/BF01725541. 
9. ↑ Krantz, Philip; Kjaergaard, Morten; Yan, Fei; Orlando, Terry P.; Gustavsson, Simon; Oliver, William D. (2019). "A quantum engineer's guide to superconducting qubits". Applied Physics Reviews 6 (2). doi:10.1063/1.5089550.